This is one basic technique that can be used to make magic squares whose side length is odd: 3, 5, 7, 9, …
- Draw the table.
- Put the number 1 below the center cell.
- Put the next numbers to the right on the row below, wrapping around when necessary.
- When the next cell is already filled, put the next number two rows below, wrapping around when necessary.
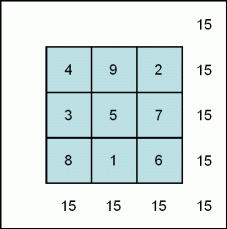
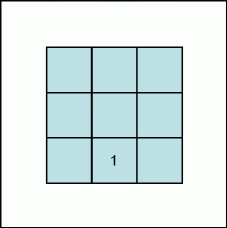
So to make a 3 by 3 square, the first step is to draw the table and put the number 1 under the center cell.
Then put the number 2 to the right and below number 1. Number 2 ends up in the upper right cell, as it is necessary to wrap around when the move exceeds the last row of the table. Accordingly, number 3 ends in the middle left cell, after wrapping around when the move exceeds the right column of the table.
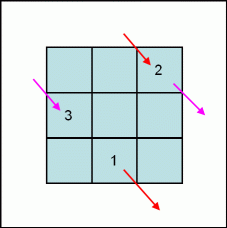
As the cell to the right and below number 3 is already filled by number 1, number 4 ends two rows below number 3. With the wrap around, this means the upper left cell of the table.
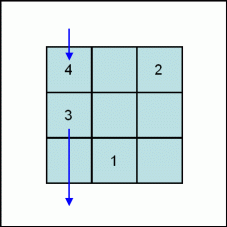
From then we can resume the below-right move, with one more transition by the 2-rows-below move when the next cell below-right number 6 is already filled by number 4.
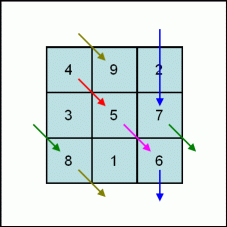
When all the cells are filled, the result is a 3 by 3 magic square. The sums of the numbers in each row, each column and each diagonal are all equal to 15.